Blogspot Wadek III

Klik disini

Blogspot Jurusan Ekonomi Pembangunan

Klik disini

Uji Stasioneritas data Time Series lengkap

Dalam berbagai studi ekonometrik, data time series paling banyak digunakan. namun, penggunaan time series tidak lepas dari permasalahan autokorelasi yang sudah dibahas sebelumnya. tetapi kali ini kita tidak akan membahas autokorelasi lagi. kali ini kita akan bahas bentuk lain dari autokorelasi yaitu stasioneritas. karena autokorelasi mengakibatkan data menjadi tidak stasioner.

Penentuan stasioner ini sangatlah penting. Hal ini berkaitan dengan dengan metode estimasi yang digunakan. Seperti yang sudah dijelaskan sebelumnya bahwa jenis data yang digunakan akan menetukan estimasi yang digunakan. namun secara umum banyak metode dalam membuat model-model ekonometrik dengan data time series yang mengharuskan kita menggunakan data yang stasioner. jadi, patutlah kita mengatakan stasioneritas menjadi masalah penting dalam analisis data time series.

Ide dasar dari stasioneritas adalah hukum probabilitas mengharuskan proses tidak berubah sepanjang waktu, dengan kata lain proses dalam keadaan setimbang secara statistik (Cryer, 1986).

Sekumpulan data dinyatakan stasioner jika nilai rata-rata dan varian dari data time series tersebut tidak mengalami perubahan secara sistematik sepanjang waktu, atau sebagian ahli menyatakan rata-rata dan variannya konstan (nachrowi dan haridus usman, 2006).

Sebelum kita masuk dalam uji stasioneritas, perlu kita mengetahui beberapa model time series stokastik yang tidak stasioner:

1. Random walk tanpa intersep

Random walk tanpa intersep akan mengalami rata-rata konstan pada awalnya, namun nilai variansnya meningkat sejalan dengan bertambahannya waktu.
 

2. Random walk dengan intersep

Sedangkan random walk dengan intersep tidak hanya variansnya yang tidak konstan tetapi juga rata-ratanya meningkat sejalan dengan bertambahnya waktu.



3. Random walk dengan trend

salah satu variasi model random walk adalah dengan menambahkan trend dengan modelnya. sehingga modelnya berubah menjadi:


berdasarkan hasil tersebut. walaupun nilai variansnya konstan namun nilai rata-ratanya berubah sepanjang waktu. sehinga model masih belom stasioner.


4. Random walk dengan intersep dan trend

dengan adanya intersep pada model random walk trend akan mengakibatkan rata-rata dan variansnya tidak konstan.

Pengujian stasioneritas:

1. Grafik

Untuk melihat adanya stasioneritas dapat dengan mudah kita lihat dengan grafik. grafik tersebut dibuat plot antara observasi dengan waktu. jika terlihat memiliki rata-rata dan varians konstan, maka data tersebut dapat disimpulkan stasioner. berikut contoh metode grafik yang merupakan data stasioner:



2. Korelogram

Metode grafik diatas memiliki kelamahan dalam objektivitas peneliti. karena setiap peneliti memiliki pandangan yang bisa berbeda-beda. sehingga, dibutuhkan uji formal yang akan menguatkan keputusan secara ilmiah. salah satu uji formal tersebut adalah korelogram. pada dasarnya korelogram merupakan teknik identifikasi stasioner data time series melalui fungsi autokorelasi(ACF). didapat dengan membuat plot antara ρk dan k (lag). Plot antara ρk dan k ini disebut korelogram populasi. Dalam praktek, kita hanya dapat menghitung fungsi otokorelasi sampel (Sample Autocorrelation Function). untuk data yang stasioner, korelogram menurun dengan cepat seiring dengan meningkatnya k. Sedangkan untuk data yang tidak stasioner, korelogram cenderung tidak menuju nol (turun lambat)


Correlogram ini hampir sama dengan metode grafik, karena masih menggunakan unsur subjektivitas. oleh karena dasar metode ini digunakanlah beberapa metode formal yang dilakukan untuk menguji hipotesis ρk. dimana hipotesisnya sebagai berikut
h0 :ρk = 0
h1 :ρk ± 0
sehingga apabila terima h0 maka dapat dikatakan data yang digunakan sudah stasioner.

Metode formal yang dimaksud di atas dalam mendeteksi stasioneritas menggunakan korelogram:

• Uji bartlet

Bartlett menunjukkan bahwa jika suatu time series dibentuk melalui proses white noise, maka sampel otokorelasi-nya akan berdistribusi normal dengan mean 0 dan standar deviasi 1/ T½, dimana T banyaknya pengamatan, bila ada rk > 0.2 (dua kali standar deviasi), maka kita yakin dengan kepercayaan 95% bahwa ρ ± 0 dan berarti time series yang sedang kita analis bukan berasal dari proses white noise. Atau secara matematis dituliskan dengan: rk ± Zα/2 s.e

• Uji box-pierce

Uji ini digunakan untuk mengetahui apakah nilai ρk pada sekumpulan waktu secara nyata berbeda dengan 0.
untukk menguji hipotesis tersebut tersebut, kita gunakan tes Q yang dikenalkan oleh Box dan Pierce,



• Uji Ljung-Box

Sejatinya uji ini hampir bisa dibilang kembar. namun, uji ini lebih "powerful". uji ini cocok untuk sampel yang berukuran kecil
untuk penetuan penolakan hipotesis, hampir sama dengan uji diatas.

Uji unit root

kedua metode diatas masih menggunakan subjektivitas sehingga diperlukan uji formal. uji formal ini disebut uji unit root. uji ini yang paling sering digunakan dalam melakukan uji stasioneritas. uji ini disebut Dickey-Fuller (DF) test sesuai dengan yang menciptakan yaitu David Dickey dan Wayne Fuller.dimana menggunakan persamaan berikut:

sehingga akan membentuk hipotesis sebagai berikut:

H0: δ = 0
H1: δ ≠ 0

Jika kita tidak menolak hipotesis δ = 0, maka ρ = 1. Artinya kita memiliki unit root, dimana data time series Yt tidak stasioner.

Pada penerapannya, ada tiga bentuk persamaan uji Dickey-Fuller sebagai berikut:

1. Model tanpa intersep
2. Model dengan intersep
3. Model dengan intersep dan memasukkan variabel bebas waktu.

hal ini penting karena akan menetukan model yang digunakan. penetuan dengan atau tanpa intersep tergantung dari datanya. yang akan digunakan untuk pemilihan model pada software statistik misalnya EViews. secara umum kita bisa mencobanya masing-masing model sehingga keputusanya akan lebih tepat.

Model-model sebelumnya mengasumsikan erorr(ut) tidak berkorelasi, Hampir tidak mungkin. Untuk mengantisipasi adanya korelasi tersebut, Dickey-Fuller mengembangkan pengujian diatas dengan sebutan: Augmented Dickey-Fuller (ADF) Test
formulasinya sebagai berikut:

Berdasarkan model tersebut kita dapat memilih tiga model yang akan digunakan untuk melakukan Uji ADF, model tersebut sama dengan model ADF di atas. Penjelasan lengkap mengenai uji tersebutdapat dilihat pada Gujarati (2004) halaman 814-818.

Mengatasi Ketidakstasioneran Data Time Series

Apabila suatu data runtun waktu (time series) tidak stasioner atau memilki akar unit, ada beberapa trik yangg dapat dilakukan untuk menstasionerkan data tersebut. Salah satu caranya adalah dengan proses difference stokastik, yaitu dengan mengurangkan set data runtun waktu dengan akar unitnya. Misalkan suatu data runtun waktu memiliki persamaan akar unit:



Maka proses difference stokastiknya adalah,

Data runtun waktu yang tidak di-difference-kan sering juga disebut sebagai data level dan memiliki lambang difference I(0). Sedangkan untuk data yang telah di-difference-kan pada orde ke-n memiliki lambang difference I(n). Proses difference stokastik akan mengubah data runtun waktu yang tadinya tidak stasioner menjadi data runtun waktu yang stasioner dan memiliki rata-rata serta varians yang konstan antar periodenya.
Proses difference stokastik merupakan salah satu bentuk transformmasi data. Ada beberapa bentuk lain transformasi suatu data, antara lain, transformasi ke bentuk logaritma (log), logaritma natural (ln), standarisasi (z-score), dll. Tujuan dari transformasi yang lain tersebut biasanya bukan untuk meghilangkan akar unit atau menstasionerkan data, tetapi menghilangkan efek satuan, menormalkan data, dsb. Namun, biasanya, data yang ditransformasi ke bentuk2 tersebut juga menjadi stasioner.

Sumber: Klik disini

 

nb;
untuk tutorialnya ada disini gan..[tutorial]-uji-stasioneritas-dengan-eviews
untuk uji stasioner data panel disini Uji Stasioner (unit root) untuk Data Panel

Tutorial Uji stasioneritas dengan EViews

Sebelumnya telah kita bahas secara teori bagaimana uji stasioner. kali ini kita akan membahas langkah-langkah uji stasioneritas dengan menggunakan EViews 6.0. langsung aja ya kita saksikan.

Langkah-Langkah Uji stasioneritas dengan EViews

1. Masukkan data yang akan digunakan. Dengan mengikuti langkah berikut.

2. Pilih file workfile yang akan digunakan. Dan selajutnya next-next aja. sehingga akan menghasilkan data sebagai berikut.

3. Klik dua kali salah satu variabel yang akan diuji. Hasilnya sebagai berikut:

4. Setelah ini kita akan melakukan langkah-langkah menetukan pengujian. Sesuai yang dijelaskan pada materi sebelumnya. Ada beberapa cara untuk menentukan stasioneritas. Maka pada tahap ini kita akan mencoba satu-satu.

a. Grafik

1. Pilih view, kemudian graph. Sesuai gambar berikut:

Setelah itu langsung ok aja. Kalau mau diubah-ubah bisa juga. Hasilnya sebagai berikut:

Berdasarkan gambar diatas terlihat bahwa adanya indikasi datanya stasioner. Hal itu terlihat dari grafiknya berada disekitar rata-rata atau dengan kata lain rata-rata dan varians konstan.

b. Correlogram

1. Hampir sama dengan sebelumnya. Pilih view kemudian correlogram. Seperti gambar berikut:

2. Kemudian muncul gambar berikut: pilih level untuk stasioner data level untuk 1st difference untuk data first difference, dst. Sedangkan untuk lag-nya untuk melihat sampai lag keberapa mau dilihat. Berbeda dengan SPSS, EViews bisa ditentukan sendiri lag-nya.

3. Hasilnya sebagai berikut:

Berdasarkan hasil tersebut terlihat bahwa correlogram secara cepat menuju nol, sehingga dikatakan datanya stasioner. Dilihat Q-stat terlihat bahwa nilainya signifikan artinya datanya stasioner sesuai dengan materi sebelumnya.

c. Unit Root test

Kali ini kita melangkah ke uji formal yang biasa kita gunakan dalam penelitian ilmiah. Disini ada beberapa metode yang akan digunakan sehingga akan dibahas masing-masing.

1. Sama dengan sebelumnya. Dengan view dan unit root.

2. Kemudian menetukan metode apa yang digunakan. Dan model apa yang digunakan. Kali ini kita menggunakan 3 metode yaitu DF, ADF, Philips-peron. Sedangkan untuk medolnya bisa dicoba-coba.

Hasil uji 3 metode tersebut adalah sebagai berikut:

a. DF (Dickey-Fuller)

Berdasarkan hasil tersebut terlihat bahwa nilai ADF lebih kecil dari nilai kritisnya sehingga tolak h0 sehingga datanya stasioner.

b. ADF (Augmented Dickey Fuller)

Sama dengan DF, menunjukkan bahwa datanya stasioner.

c. Philips perron

Berdasarkan hasil tersebut data masih menunjukkan stasioner, tapi signifikan pada 5%.


5. Kesimpulan data yang kita gunakan menunjukkan datanya stasioner dengan menggunakan beberapa metode diatas.

Sumber:

Klik disini

Tutorial Eviews Error Correction Mechanism (ECM)

Pada postingan sebelumnya suda dijelaskan beberapa hal mengenai Error Correction Mechanism (ECM). Nah, pada post ini akan dipaparkan praktek eviews, tahap-tahap ECM yang sudah dijelaskan sebelumnya di Teori ECM. Untuk tutorial, silahkan download datanya di sini.

Lebih jelas mengenai praktek tahap-tahap ECM tersebut dalam eviews adalah sebagai berikut:

I. Pengecekan Stasioneritas

Hal penting yang harus diingat ketika menganalisis data time series adalah mengutamakan pengecekan stasioneritas datanya sebelum diproses lebih lanjut (lebih detail mengenai uji stasioneritas menggunakan eviews bisa dilihat di postingan ini).
Khusus untuk metode ECM, pastikan seluruh variabel yang digunakan, tidak ada yang stasioner pada Level. Oleh karena itu, tahap pertama dalam tutorial ini adalah menguji stasioneritas seluruh variabel. Supaya lebih memudahkan, stasioneritasnya tidak usah dicek satu-satu tapi secara bersamaan. Caranya, pada Workfile ECM, block semua variabel yg ingin digunakan, klik kanan lalu pilih Open > as Group. Setelah itu akan muncul tampilan seperti gambar di bawah:

Selanjutnya, pada window baru, klik View > Unit Root Test, dan kemudian akan muncul window dengan nama "Group Unit Root Test" seperti gambar di bawah. Untuk tahap awal, set tipe data ke Level.

Untuk uji stasioneritas kumpulan variabel ini, yang berbeda dengan 1 variabel adalah Test Type-nya (kotak hijau). Supaya stasioneritas masing-masing variabel bisa dicek, pilih Test Type yang ada kata "Individual..."-nya. Setelah itu klik OK, yang lain tidak usah diubah.
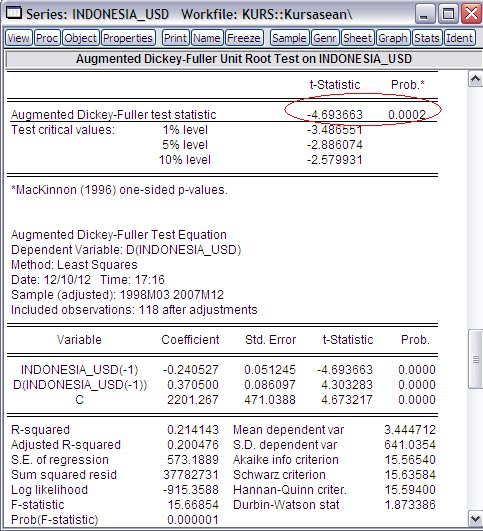
Berikutnya akan muncul window yang berisi output seperti:

Bagian yang perlu diperhatikan adalah kolom Probability yang posisinya paling bawah output. Karena hasil pengujian yang diinginkan adalah seluruh variabel tidak stasioner pada Level, nilai probabilitas masing-masing variabel harus lebih besar dari alpha yang ditetapkan.
Misalnya kita pakai alpha=0.05, karena semua nilainya memang lebih besar dari 0.05, semua variabel tidak ada yg stasioner pada Level dan penerapan metode ECM, boleh dilanjutkan.

Agar lain kali bisa langsung dilihat, jangan lupa outputnya disimpan. Caranya, klik Freeze, setelah itu akan muncul window baru yang tampilannya sama. Di window baru, klik Name, terserah teman2 outputnya mau dinamai apa. Output yang disimpan tadi akan muncul sebagai objek baru dengan simbol 

Untuk output2 berikutnya, kalau mau disimpan, silahkan pakai cara tersebut.

Kalau sudah dipastikan tidak ada yang stasioner di Level, ulangi langkah uji stasioneritasnya tapi dengan data 1st difference (gambar 2). Untuk contoh yg saya berikan, semua variabelnya stasioner pada tahap ini (difference pertama), sehingga pada output berikutnya, nilai kolom Probability semua variabel berada di bawah 0.05.

Misalkan saja ada kasus dimana 1 saja variabel tidak stasioner pada difference pertama seperti yg lain, maka kita harus men-difference-kan semua variabel lagi ke 2nd difference dan seterusnya, sampai semuanya stasioner.

II. Estimasi persamaan jangka panjang

Variabel-variabel yang ingin digunakan dan telah memenuhi syarat pada tahap 1, pada tahap ini akan dibuat persamaan regresinya, dengan Y sebagai variabel terikat sedangkan sisanya, semua sebagai variabel bebas. Kembali ke Workfile ECM, block lagi semua variabelnya pilih Open > as Equation..., setelah itu akan akan muncul window tempat kita mengisi persamaan. Tulis persamaannya persis seperti gambar di bawah:

Pilihan yang lain tidak perlu diubah, setelah tulis persamaan langsung klik OK. Berikutnya akan muncul output yang berisi estimasi dari koefisien2 tiap variabel bebas. Perhatikan nilai2 signifikansi yang dilingkari pada gambar di bawah:

Cek nilai F-statistic (kotak hijau) lebih dulu, kalau memang sudah lebih kecil dari alpha (0.05), barulah bisa kita cek nilai signifikansi masing2 variabel (kotak biru). Signifikansi masinng2 variabel tidak harus semuanya berada di bawah 0.05, kalau di dalam suatu penelitian, hal tersebut tergantung pada kajian teorinya. Namun, apabila nilai probabilitas suatu variabel bebas berada di bawah 0.05, maka variabel bebas tersebut dikatakan berpengaruh terhadap variabel terikatnya.

III. Pengecekan Kointegrasi

Pada teori mengenai ECM sebelumnya telah dijelaskan bahwa kointegrasi suatu persamaan regersi dapat dilihat dari residualnya. Apabila residual stasioner, terdapat kointegrasi.
Pada workfile ECM ada variabel dengan nama resid, yang merupakan tempat menyimpan residual persamaan yang baru saja diestimasi, sehingga nilainya berubah-ubah. Padahal residual persamaan jangka panjang, akan diuji stasioneritasnya dan digunakan sebagai variabel pada persamaan berikutnya. Oleh karena itu, langsung setelah estimasi persamaan jangka panjang, kita harus menyimpa residualnya dalam bentuk variabel baru yang tetap. Caranya adalah meng-generate variabel baru yg nilainya sama dengan variabel resid. Misal kita buat variabel baru tersebut dengan nama res menggunakan perintah seperti gambar di bawah lalu klik enter:

Variabel baru dengan nama res tersebut kemudian kita uji stasioneritasnya seperti pada langkah pertama, klik kanan di variabelnya, Open, di window baru pilih View > Unit root test, pilih tipe data Level  lalu klik OK. Apabila kolom Prob* berisi nilai di bawah alpha (0.05), maka kita bisa lanjut ke estimasi persamaan jangka pendek.

Output di atas memberikan informasi bahwa variabel res stasioner pada Level, dan secara tersirat menyatakan bahwa Y, X1, X2, X3, X4, X5, dan X6 sailing berkointegrasi.

IV. Estimasi persamaan jangka pendek

Pada tahap ini, buat lagi persamaan regresi menggunakan variabel-variabel sebelumnya (tapi yg sudah distasionerkan) ditambah variabel res (tahun sebelumnya). Caranya, munculkan lagi window untuk memasukkan persamaan dengan memilih "Estimation Equation..." yang ada pada menu Quick (paling atas). Setelah itu akan muncul tampilan:

Karena variabel Y, X1, X2, X3, X4, X5, dan X6 stasioner pada difference pertama, gunakan transformasi variabel-variabel tersebut ke bentuk difference pertama dalam persamaan. Jangan lupa menyertakan variabel res(-1) yg merupakan residual pada tahun sebelumnya. Tuliskan persamaan persis seperti pada kotak merah gambar di atas lalu klik OK. Setelah itu akan muncul output sepert ini:

Untuk persamaan jangka pendek, pertama-tama pastikan nilai probabilitas F-statistic berada di bawah alpha (0.05). Setelah itu, cek speed of adjustment-nya (koefisien dari res(-1)). Nilai koefisien tersebut harus negatif dan signifikan (probabilitasnya berada di bawah 0.05). Barulah kemudian kita cek probabilitas masing-masing variabel, yg mana saja yang nilainya signifikan atau berada di bawah alpha (0.05), sama seperti pada persamaan jangka panjang.

V. Pengecekan Asumsi

Tahap ini sebenarnya adalah tahap yang harus ada untuk semua metode yang menggunakan regresi dalam proses analisisnya. Pada bagian teori ECM juga hanya disinggung sedikit karena nanti akan dibahas satu-satu beserta tutorialnya pada postingan yang berbeda.

VI. Interpretasi

Setelah seluruh tahap-tahap ECM terpenuhi kita mendapatkan 2 persamaan yang menjadi inti dari digunakan metode ini. Dari sinilah pengaruh variabel-variabel bebas terhadap variabel terikat yang ingin kita teliti, dapat dijelaskan.
Berdasarkan output persamaan jangka panjang, didapatkan:

Yt = -8.0993 + 0.7422 X1t* - 0.3207 X2t* + 0.9738 X3t* + 0.4464 X4t - 0.1172 X5t* - 0.0253 X6t

ket : (*) --> variabel yang signifikan (<0.05)
        (t) --> periode atau tahun 


Persamaan ini hanya dapat memberikan kita informasi bahwa dalam jangka panjang, X1, X2, X3, dan X5 berpengaruh signifikan terhadap Y.

Sedangkan dari output persamaan jangka pendek, didapatkan:

ΔYt = 0.0025 + 0.4157 ΔX1t* - 0.3156 ΔX2t* + 1.0558 ΔX3t* + 0.0816 ΔX4t - 0.0739 ΔX5t* - 0.0741 ΔX6t - 0.6899 RESt-1

Persamaan tersebut memberikan kita informasi bahwa dalam jangka pendek, X1, X2, X3, dan X5 berpengaruh signifikan terhadap Y.

1. Kenaikan perubahan X1 sebesar 1 unit akan menyebabkan kenaikan perubahan Y sebesar 0.42 unit,
2. Kenaikan perubahan X2 sebesar 1 unit akan menyebabkan penurunan perubahan Y sebesar 0.32 unit,
3. Kenaikan perubahan X3 sebesar 1 unit akan menyebabkan kenaikan perubahan Y sebesar 1.06 unit, dan
4. Kenaikan perubahan X5 sebesar 1 unit akan menyebabkan penurunan perubahan Y sebesar 0.07 unit

Berdasarkan nilai speed of adjustment, ada sebesar 69% ketidakseimbangan, pada pengaruh jangka pendek X1, X2, X3, X4, X5, dan X6 terhadap Y, yg terkoreksi setiap periodenya.

Sumber:

Klik disini

Teori Error Correction Mechanism (ECM)

Error Correction Mechanism (ECM) merupakan analisis data time series yang digunakan untuk variabel-variabel yang memilki ketergantungan yang sering disebut dengan kointegrasi. Metode ECM digunakan menyeimbangkan hubungan ekonomi jangka pendek variabel-variabel yang telah memiliki keseimbangan/hubungan ekonomi jangka panjang.

Apa itu Kointegrasi?

Analisis data time series mensyaratkan stasioneritas sebagai salah satu dasar penting keabsahan prosesnya. Pada postingan sebelumnya, telah dibahas sedikit mengenai teori dan cara mengecek stasioneritas pada suatu data time series (bagi yang belum baca, silahkan cek di sini). Berkaitan dengan topik tersebut, terdapat keadaan dimana kita dapat menganalisis hubungan variabel-variabel time series, walaupun ketika variabel-variabel tersebut tidak stasioner, yaitu ketika kombinasi linier variabel2 tersebut, stasioner. Kondisi tersebut dikenal sebagai kointegrasi. Misalkan ketika kita menganalisis pengaruh pendapatan (misal dilambangkan X) terhadap konsumsi (dilambangkan dengan Y), dengan kondisi kedua variabel tersebut tidak stasioner. Namun ketika variabel tabungan (dilambangkan dengan E), yang merupakan kombinasi linier dari X dan Y (E=X-Y), stasioner, X dan Y dikatakan saling berkointegrasi. Apabila dijelaskan dalam gambar, maka pergerakan Y dan X akan seperti ini:

Sepeti terlihat pada gambar, ciri khas dari variabel-variabel yang berkointegrasi adalah pergerakan yang sama atau beriringan. Oleh karena itu, pergerakan variabel E yang merupakan hasil X-Y akan stasioner seperti gambar di bawah:

Menurut Enders (2004) terdapat beberapa karakteristik penting mengenai kointegrasi beberapa variabel, yaitu: 

1. Kointegrasi mengacu pada kombinasi linier dari variabel-variabel nonstasioner.
2. Semua variabel yang terkait harus dalam orde integrasi yang sama.
3. Jika xt memiliki n komponen, maka ada sebanyak n-1 kombinasi linier yang mungkin terjadi → n-1 vektor kointegrasi yang mungkin.
4. Kebanyakan kajian kointegrasi fokus pada variabel dengan l(d=1) karena jarang sekali variabel-variabel dalam ekonomi yang terintegrasi pada orde d>1.

*I(d=1) → difference pertama

Pengujian kointegrasi antara variabel bertujuan menunjukkan adanya hubungan atau keseimbangan jangka panjang pada variabel bebas terhadap variabel terikat. Akan tetapi, di dalam jangka pendek terdapat kemungkinan bahwa antar variabel tersebut terjadi ketidakseimbangan. Ketidakseimbangan inilah yang sering kita temui dalam perilaku ekonomi, dimana hal ini disebabkan ketidakmampuan pelaku ekonomi untuk segera menyesuaikan perubahan-perubahan yang terjadi dalam perilaku variabel ekonomi (Harris dan Sollis, 2003). Karena ketidakseimbangan inilah Error Correction Mechanism (ECM) digunakan. ECM memanfaatkan residual/error dari hubungan jangka panjang untuk menyeimbangkan hubungan jangka pendeknya. Oleh karena itu, dinamakan error correction.

 Sejarah singkat tentang ECM

Istilah Error Correction Mechanism (ECM) sudah diperkenalkan sejak tahun 1950an oleh beberapa pakar ekonometrik. Metode ini pertama kali digunakan oleh Prof. Dennis Sargan dalam penelitiannya tentang upah dan harga di UK. Dalam perkembangannya, metode ini kemudian dipopulerkan oleh Engle-Granger. 

Keuntungan ECM sebagai model dinamik dalam analisis data runtun waktu:

1. ECM dapat melakukan spesifikasi model atas bentuk umumnya, 
2. ECM dapat menjelaskan informasi jangka panjang dan jangka pendek dari data (Vamvoukas, 1998), serta dapat diketahui konsisten tidaknya model empirik dengan teori ekonomi, 
3. ECM sebagai salah satu model dinamik untuk mencari penyelesaian data runtun waktu yang tidak stasioner
4. mencari penyelesaian masalah multikolliniaritas dan regresi lancung (Insukindro (1992:14, 1999:2), Thomas (1997:388 – 390)).

Tahap-Tahap  Penerapan ECM

1) Cek stasioneritas seluruh variabel → kalau tidak memenuhi syarat tadi, ECM tidak bisa digunakan

2) Estimasi persamaan jangka panjang → persamaan jangka panjang pada ECM adalah persamaan regresi biasa dengan variabel y dan x, yang tidak stasioner pada level. Kemudian, error (e) pada persamaan regresi jangka panjang inilah yang menentukan adanya kointegrasi atau tidak pada variabel y dan x tersebut. Apabila e stasioner pada level, maka y dan x saling berkointegrasi. Persamaan jangka panjang ini sering disebut sebagai persamaaan keseimbangan dan hanya dapat digunakan apabila residual/error (e)-nya stasioner pada level. 

3) Uji kointegrasi → cek stasioneritas dari residual/error (e), kalau stasioner di level, ECM-nya dilanjutkan

4) Persamaan jangka pendek → e yang stasioner pada persamaan jangka panjang, tidak digunkan hanya untuk mengetahui ada tidaknya kointegrasi tapi juga digunakan sebagai salah satu variabel pada persamaan jangka pendek. Persamaan jangka pendek juga menggunakan variebel2 yang sama dengan variabel2 yang ada pada persamaan jangka panjang, hanya saja variabel2 tersebut telah distasionerkan, semuanya pada orde yang sama. Mungkin akan lebih dimengerti lewat persamaan berikut:

Koefisien γ pada persamaan di atas yang juga sering disebut sebagai speed of adjustment merupakan kecepatan residual/error (e) pada periode sebelumnya untuk mengoreksi perubahan variabel y menuju keseimbangan pada periode selanjutnya.

Nah, pada tahap ini ada syarat terakhir yang harus dipenuhi supaya ECM-nya sah; Koefisien γ harus signifikan dan negatif (referensinya mungkin bisa dilihat di buku Ekonometrik edisi 5 punyanya Baltagi).

Persamaan jangka panjang pada metode ECM memilki keterbatasan interpretasi, sedangkan persamaan jangka pendeknya bebas diinterpretasikan, tentu saja dengan pengujian asumsi2 regresi dulu sebelumnya. Koefisien regresi pada persamaan jangka panjang hanya dapat diinterpretasi berdasarkan arah pengaruhnya, positif atau negatif.

Sumber:

Enders, Walter. (2004). Applied Econometrics Time Series (2rd ed). New York: Wiley.

Gujarati, Damodar N. (2004). Basic Econometrics, (4th ed). The McGraw−Hill Companies. 

Greene, Wlliam H. (2003). Econometric Analysis (5th ed). New York: Prentice Hall.

Baltagi, Badi H. (2011). Econometrics (5th ed). New York. Springer.

http://statistikceria.blogspot.co.id/2014/02/error-correction-mechanism-ecm.html

Cara Input Data Panel Dengan EViews 7

Cara Input Data Panel Dengan EViews 7 (How to Input Pooled Data In Eviews 7)

Oleh : Jul Fahmi Salim

Assalamualaikum wr wb....

Selamat Pagi....

Setelah beberapa waktu vakum tidak sharing masalah pengolahan data, nah sekarang kembali lagi..heheheh

Sebelumnya share Regresi Linear Berganda dengan Shazam danCara Sinkron data + OLS dengan Shazam

Kali ini saya akan share bagaimana cara input data panel yang sebelumnya sudah beberapa kali mencoba tetapi gagal dan banyaknya permintaan dari pengunjung blog ini yang ingin postingan berupa data panel, maklum masih sama-sama belajar jadi masih banyak terdapat kekurangan...

Berikut merupakan langkah-langkahnya :

• Pastikan anda memiliki data yang akan di olah, karena jika tidak ada maka tidak akan ada yang bisa di olah.hahhahahaha (Becanda,,becandaaa)
• Buka file excel ,kemudian ketik lah data yang akan di olah
• dalam hal ini saya menggunakan data (contoh saja) Y X1 dan X2 beberapa Provinsi di Pulau Sumatera, dan susunlah data seperti di bawah ini..

• Ctrl A, (atau di blok semua data yang akan di gunakan) kemudian klik kanan
• Format cell => Number => Ok

• File => Save as

• Pilih Save as type nya Excel 97-2003 workbook=> klik Ok
• Kemudian Close file excel

Kemudian kita selanjutnya bekerja di EViews

• File => New => workfile
• isi "start date" dengan tahun awal dan "end date" untuk tahun akhir data (sebagai contoh data saya dimulai pada tahun 2007 dan berakhir tahun 2011) => klik ok

• Kemudian Pilih Object => New Object

• Pada "Type of Object" Pilih Pool dan isi "Name for Object" sesuai keinginan => klik ok

• Setelah itu maka akan keluar jendela "Pool", kemudian dibawah tulisan cross section Identifiers below.... di isi dengan nama (objek) misalnya disini saya menggunakan nama Provinsi, untuk setiap penulisan objek di awali tanda "_" (underscore)

• Setelah di isi kemudian klik menu Proc => Import pool data

• Pilih data yang akan diinput (misalnya data saya namya PANEL) => kemudian klik Open

• Untuk upper-left data cell isi sesuai dengan permulaan data berada, misalnya di cell B2 (jika data anda dimulai pada cell lainnya misalnya pada C2 maka isi dengan C2) pada excel

• untuk kotak "ordinary and pool" isikan semua var dependen dan independen diikuti tanda tanya "?"  (dalam hal ini saya menggunakan variabel Y X1 X1 dan saya input menjadi y? x1? x2?) kemudian =>> klik Ok

Jika data berhasil di input maka hasilnya akan seperti ini...

Untuk cek data apakah sudah masuk atau tidak, begini caranya :

• Blok semua objek dari "x1_aceh sampai y_sumut" 
• klik kanan =>> open as group

Setiapa Variabel data sudah terisi

• Nah jika sudah terisi maka data panel siap untuk di regresi, baik common effect, fixed effect, redundant test, uji hausman maupun random effect

Untuk Melihat Videonya klik disini

Nah demikianlah cara mudah untuk menginput data panel di eviews, mohon diberikan kritik dan sarannya agar tulisan ini bisa diperbaiki dan lebih baik kedepannya..

Terimakasih kepada Bapak Dr. Abd. Jamal, M.Si atas ilmunya...

Terimakasih Sudah Berkunjung... ;-)

Sumber: Klik disini

Materi yang sama:

http://www.diassatria.com/analisis-regresi-model-data-panel/

mmmmmmm