Regresi Linier Sederhana (Ekonometrika)

Analisis Regresi 2 Peubah (Analisis Regresi Sederhana)

         Menduga rata-rata peubah tak bebas berdasarkan nilai peubah (satu) bebas yang diketahui

           a.        Diilustrasikan dengan data dari Gujarati (2003), dengan populasi beranggotakan 60 keluarga

• X_i: pendapatan/minggu per keluarga
• Y_i: konsumsi/minggu per keluarga
• i= 1, …, 60 (60 keluarga yang diamati)
1. Dari 60 keluarga tersebut dikelompokkan ke dalam 10 kelas pendapatan

Sebaran Bersyarat dari konsumsi/minggu untuk beberapa kelas pendapatan

Konsep Fungsi Regresi Populasi (PRF)

Jika diasumsikan bahwa hubungan kedua peubah tersebut linier, maka digunakan fungsi linier dari X:

Model/Persamaan Regresi

Dibutuhkan metode tertentu untuk menduga parameter model (intersep dan slope)

Arti dari Linier

•     Linier dalam peubah

•     Linier dalam parameter

1.   Linear dalam Peubah

2.   Non Linear dalam Peubah

3.   Linear dalam Parameter

            4.  Non Linear dalam Parameter

Linier dalam peubah maupun parameter

·         Di dalam analisis regresi sederhana, LINIER berarti linier dalam PARAMETER

·         Parameter berpangkat paling tinggi 1

·         Diperbolehkan pangkat lebih dari satu untuk peubah

Keduanya Linier dalam paramater: Model Regresi Linier Sederhana

Fungsi Regresi Populasi Secara Stokastik

•      Untuk model konsumsi sebagai fungsi dari pendapatan,

•      Dimungkinkan bahwa faktor selain pendapatan juga mempengaruhi konsumsi

•      Tidak semua titik tepat pada garis regresi

•      Faktor-faktor lain tsb dirangkum dalam komponen error/galat

 

                                  

                                                                        Garis                     Error/Galat

                                                               Komponen Deterministi       komponen Stokastik

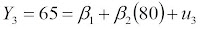
Nilai harapan di ruas kiri dan kanan dengan syarat X pada komponen stokastik

Nilai harapan konstan adalah konstan itu sendiri

 

                             Tujuan dari analisis regresi

 

                                                    Asumsi utama untuk galat/error

Keutamaan dari Komponen Stokastik Galat/Error

Mengapa tidak menggunakan sebanyak-banyaknya peubah yang mungkin mempengaruhi konsumsi? (Tidak hanya pendapatan)?

a.       Teori yang belum pasti

b.      Ketidaktersediaan data

c.       Peubah utama vs peubah tambahan

d.      Sifat alami perilaku manusia (acak)

e.       Peubah proxy yang kurang berkualitas

f.       Model sesederhana mungkin (Principle of Parsimony)

g.      Kemungkinan hubungan fungsional yang kurang tepat

Fungsi Regresi Sampel (Sample Regression Function – SRF)

1. Data pendapatan dan konsumsi: diasumsikan berasal populasi 60 keluarga
2. Fungsi Regresi Populasi (PRF)
3. Secara praktek: tidak mungkin memperoleh informasi secara keseluruhan dari populasi
4. Pengambilan sampel pasangan nilai pendapatan (X) dan konsumsi (Y) dari populasi tersebut
5. Menduga PRF berdasarkan informasi dari sampel
6. Akibat fluktuasi sampel: kemungkinan pendugaan tidak akurat

Pasangan konsumsi dan pendapatan dari  2 sampel berukuran 10 keluarga yang diambil dari populasi 60 keluarga

Garis regresi dari dua sampel yang berbeda tersebut:

       a.       Dua garis yang berbeda

       b.      Fungsi Regresi Populasi Dalam prakteknya tidak akan pernah diketahui

Fungsi Regresi Sampel (SRF)

a.    Regresi yang dibentuk dari sampel

b.    Dipakai untuk menduga regresi populasi

c.    Tidak akan pernah sama untuk sampel yang berbeda

    

      

Untuk masing-masing titik

    Komponen galat sampel dengan asumsi yang sama seperti                                                                             galat populasi

Tujuan Analisis Regresi

             a.      Menduga PRF dengan SRF

2. Dengan adanya sampel yang berfluktuasi, SRF hanya pendekatan dari PRF

 SRF underestimate PRF untuk X di kiri titik A

SRF overestimate PRF untuk X di kanan titik A

 

Sumber: Klik disini